Перпендикулярные прямая и плоскость, признак и условия перпендикулярности прямой и плоскости. Признак перпендикулярности прямой и плоскости: теория и практика Текстовая расшифровка урока

Определение. Прямая пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна данной плоскости.
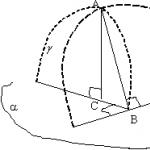
Доказательство. Пусть а – прямая перпендикулярная прямым b и с , принадлежащим плоскости a . А – точка пересечения прямых. В плоскости a через точку А проведем прямую d , не совпадающую с прямыми b и с . Теперь в плоскости a проведем прямую k , пересекающую прямые d и с и не проходящую через точку А. Точки пересечения соответственно D, В и С. Отложим на прямой а в разные стороны от точки А равные отрезки АА 1 и АА 2 . Треугольник А 1 СА 2 равнобедренный, т.к. высота АС является так же и медианой (признак 1), т.е. А 1 С=СА 2 . Подобно в треугольнике А 1 ВА 2 равны стороны А 1 В и ВА 2 . Следолвательно, треугольники А 1 ВС и А 2 ВС равны по третьему признаку Поэтому равны углы А 1 ВD и А 2 ВD. Значит, равны и треугольники А 1 ВD и А 2 ВD по первому признаку . Поэтому А 1 D и А 2 D. Отсюда треугольник А 1 DА 2 равнобедренный по определению. В равнобедренном треугольнике А 1 D А 2 D А – медиана (по построению), а значит и высота, то есть угол А 1 АD прямой, а значит прямая а перпендикулярна прямой d . Таким образом можно доказать, что прямая а перпендикулярна любой прямой проходящей через точку А и принадлежащей плоскости a . Из определения следует, что прямая а перпендикулярна плоскости a .

Построение прямой перпендикулярной данной плоскости из точки, взятой вне этой плоскости.
Пусть a - плоскость, А – точка, из которой надо опустить перпендикуляр. В плоскости проведем некоторую прямую а . Через точку А и прямую а проведем плоскость b (прямая и точка определяют плоскость, причем только одну). В плоскости b из точки А опустим на прямую а перпендикуляр АВ. Из точки В в плоскости a восстановим перпендикуляр и обозначим прямую, на которой лежит этот перпендикуляр за с . Через отрезок АВ и прямую с проведем плоскость g (две пересекающиеся прямые определяют плоскость, причем только одну). В плоскости g из точки А опустим на прямую с перпендикуляр АС. Докажем, что отрезок АС – перпендикуляр к плоскости b . Доказательство. Прямая а перпендикулярна прямым с и АВ (по построению), а значит она перпендикулярна и самой плоскости g , в которой лежат эти две пересекающиеся прямые (по признаку перпендикулярности прямой и плоскости). А раз она перпендикулярна этой плоскости, то она перпендикулярна и любой прямой в этой плоскости, значит прямая а перпендикулярна АС. Прямая АС перпендикулярна двум прямым, лежащим в плоскости α : с (по построению) и а (по доказанному), значит она перпендикулярна плоскости α (по признаку перпендикулярности прямой и плоскости)

Теорема 1 . Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны.
Доказательство. Пусть а и b - перпендикулярные прямые, а 1 и b 1 - параллельные им пересекающиеся прямые. Докажем, что прямые а 1 и b 1 перпендикулярны.
Если прямые а , b , а 1 и b 1 лежат в одной плоскости, то они обладают указанным в теореме свойством, как это известно из планиметрии.
Допустим теперь, что наши прямые не лежат в одной плоскости. Тогда прямые а и b лежат в некоторой плоскости α , а прямые а 1 и b 1 - в некоторой плоскости β . По признаку параллельности плоскостей плоскости α и β параллельны. Пусть С - точка пересечения прямых а и b , а С 1 - пересечения прямых а 1 и b 1 . Проведем в плоскости параллельных прямых а и а а и а 1 в точках А и А 1 . В плоскости параллельных прямых b и b 1 прямую, параллельную прямой СС 1 . Она пересечет прямые b и b 1 в точках B и B 1 .
Четырехугольники САА 1 С 1 и СВВ 1 С 1 - параллелограммы, так как у них противолежащие стороны параллельны. Четырехугольник АВВ 1 А 1 также параллелограмм. У него стороны АА 1 и ВВ 1 параллельны, потому что каждая из них параллельна прямой СС 1 .Таким образом четырехугольник лежит в плоскости, проходящей через параллельные прямые АА 1 и ВВ 1 . А она пересекает параллельные плоскости α и β по параллельным прямые АВ и А 1 В 1 .
Так как у параллелограмма противолежащие стороны равны, то АВ=А 1 В 1 , АС=А 1 С 1 , ВС=В 1 С 1 . По третьему признаку равенства треугольники АВС и А 1 В 1 С 1 равны. Итак, угол А 1 С 1 В 1 , равный углу АСВ, прямой, т.е. прямые а 1 и b 1 перпендикулярны. Ч.т.д.

Свойства перпендикулярных прямой и плоскости.
Теорема 2 . Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Доказательство. Пусть а 1 и а 2 - две параллельные прямые и α - плоскость, перпендикулярна прямой а 1 . Докажем, что эта плоскость перпендикулярна и прямой а 2 .
Проведем через точку А 2 пересечения прямой а 2 с плоскостью α произвольную прямую с 2 в плоскости α . Проведем в плоскости α через точку А 1 пересечения прямой а 1 с плоскостью α прямую с 1 , параллельную прямой с 2 . Так как прямая а 1 перпендикулярна плоскости α , то прямые а 1 и с 1 перпендикулярны. А по теореме 1 параллельные им пересекающиеся прямые а 2 и с 2 тоже перпендикулярны. Таким образом, прямая а 2 перпендикулярна любой прямой с 2 в плоскости α . А это значит, что прямая а 2 перпендикулярна плоскости α . Теорема доказана.

Теорема 3 . Две прямые, перпендикулярные одной и той же плоскости, параллельны между собой.
Имеем плоскость α и две перпендикулярные ей прямые а и b . Докажем, что а || b .
Через точки пересечения прямыми плоскости проведем прямую с . По признаку получаем а ^ c и b ^ c . Через прямые а и b проведем плоскость (две параллельные прямые определяют плоскость и притом только одну). В этой плоскости мы имеем два параллельные прямые а и b и секущую с . Если сумма внутренних односторонних углов равна 180 о, то прямые параллельны. У нас как раз такой случай - два прямых угла. Поэтому а || b .

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Презентации представляют некоторую последовательность кадров, содержащих текст, либо рисунок, либо то и другое.

Художник, создающий картину, видит конечную цель своего замысла. Зрители, оценивающие картину, также интересуются конечным результатом. Путь, по которому прошел художник, часто остается тайной даже для искусствоведов.

Учитель, объясняющий новую тему, напротив, заинтересован показать последовательность получения результата, его отдельные шаги, или, если можно так выразиться, «алгоритм» его получения.

Известный математик и астроном Жюль Анри Пуанкаре (1854 – 1912) объяснял свои успехи тем, что он запоминает алгоритмы, а не факты. Запомнить алгоритм, то есть логическую последовательность, проще, чем отдельный факт.

Ученик так же лучше бы понимал алгоритм. Однако учебник часто не содержит всех промежуточных этапов получения решения, особенно это касается построения рисунков. Обычно показывается окончательный рисунок, содержащий много элементов, что не способствует пониманию и запоминанию ее учеником.

Поэтапный или поэлементный показ текста и рисунка в учебнике невозможен. Это привело бы к увеличению его объема.

Существуют программы, дающие учителю возможность создания презентаций, например,

программа Power Point, имеющая богатые возможности для создания кадров и навигации. Однако в этой программе отсутствует возможность поэлементного раскрытия содержания рисунка. Рисунок показывается полностью, либо показывается какая-то его часть, а для того, чтобы последовательно показать изменения рисунка, необходимо создавать новые рисунки и показывать их последовательно, что увеличивает размер программы и требует точного совмещения положений рисунков, так как даже небольшие отклонения приводят к смещению рисунка и затрудняют его восприятие.

Между тем, существует свободно распространяемая система LaTex, включающая пакеты Beamer и Tikz, позволяющая как создавать презентации, так и постепенно показывать рисунок, не изменяя кадр целиком, а добавляя элементы рисунка. Данная возможность особенно важна при показе сложных рисунков, имеющих много элементов. При показе всего рисунка ученику сложно сразу осознать, каким образом и в какой последовательности создавались элементы рисунка, что затрудняет его понимание.

Цель данной презентации состоит в том, чтобы показать возможности, предоставляемые указанными выше пакетами, для создания постепенно раскрываемого содержания кадров (слайдов). Практическое применение подобных презентаций показало их более высокую эффективность в процессе изучения, особенно разделов, требующих рассмотрения достаточно сложных чертежей. К таким разделам относится тема «Признак перпендикулярности прямой и плоскости».

Приведем краткое содержание презентации.

Сначала показывается название презентации (слайд 1). Затем следует эпиграф, на каждом уроке различный (слайды 2, 3), а за ним цель урока (слайды 4–7), раскрываемые на экране последовательно.

1. Повторить теоретический материал предыдущего урока (слайд 4).
2. Решить задачу 119 (слайд 5).
3. Доказать признак перпендикулярности прямой и плоскости (слайд 6).
4. Показать применение признака перпендикулярности при решении задач (слайд 7).

Повторение темы «Перпендикулярные прямые».

Вопрос: Какие прямые в пространстве называются перпендикулярными (слайд 8)?

Ответ: (сначала ответов на вопросы не видно, затем они открываются на этом же слайде и выделены красным цветом)

Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90 градусов (слайды 9 (ответ) и 10 (рисунок)).

Вопрос: Что утверждает лемма о перпендикулярности двух параллельных прямых к третьей прямой (слайд 11)?

Ответ: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой (слайд 12 (ответ) и 13 (рисунок)).

Вопрос: Какая прямая называется перпендикулярной к плоскости (слайд 14).

Ответ: Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости (обозначение a ⊥ a (слайд 15)). Показывается рисунок (слайд 16).

Вопрос: Какая связь между параллельностью параллельных прямых и их перпендикулярностью к плоскости (слайд 17)?

Ответ: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости (слайд 18 (ответ) и 19 (рисунок)).

Вопрос: Как формулируется обратная теорема (слайд 20)?

Ответ: Если две прямые перпендикулярны к плоскости, то они параллельны (слайд 21).

Показывается рисунок (слайд 22).

Представьте телеграфные столбы вдоль дороги. Можно ли утверждать, что столбы перпендикулярны к плоскости дороги (слайды 23, 24, 25)?

Нельзя! Как видно на втором рисунке (вид сбоку), левый и правый столбы даже не параллельны (слайд 26).

Решим задачу № 119.

Прямая OA перпендикулярна к плоскости OBC и точка O является серединой отрезка.AD . Докажите, что а) AB= DB ; б) AB= AC , если OB= OC ; в) OB= OC , если AB= AC (слайд 27).

Решение, (случай а)) (слайд 28). Показывается рисунок (слайд 29). OA ⊥ OBC по условию (слайд 30), тогда OA ⊥ OB по определению перпендикулярности прямой к плоскости (слайд 31). OA= OD по условию задачи, поэтому OB – серединный перпендикуляр к AD и поэтому AB= DB (слайд 32).

Решение, (случай б)) (слайд 33). Показывается рисунок (слайд 34). OA ⊥ OBC по условию (слайд 35), тогд OA ⊥ OC . Если OB = OC , то ΔAOC = ΔAOB (по двум катетам) и AB= AC (слайд 36).

Решение, (случай в)) (слайд 37). Показывается рисунок (слайд 38). Если AB= AC , то ΔAOC = ΔAOB (по катету и гипотенузе) и OB= OC (слайд 39).

Вопрос: Как же проверить, перпендикулярна данная прямая к данной плоскости или нет (слайд 40)? Ответ дает теорема, выражающая признак перпендикулярности прямой и плоскости (слайд 41).

Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости (слайд 42).

Приводится краткая запись условия теоремы и ее заключения (слайды 43 - 46).

Затем показывается (пошагово) доказательство.

Рассмотрим плоскость a (слайд 47), (показывается плоскость a (слайд 48)) и прямую a , a ⊥ p , a ⊥ q , где (слайд 49) (показывается прямая a (слайд 50)), p и q – прямые, принадлежащие плоскости a , пересекающиеся в точке O (слайд 51). (Показываются прямые p ,q и точка O (слайды 52, 53)).

Пусть m произвольная прямая плоскости a (слайд 54). (Показывается прямая m (слайд 55)). Докажем, что a ⊥ m . Тогда a ⊥ a (по определению) (слайд 56).

Рассмотрим сначала случай, когда прямая a проходит через точку O (слайд 57). (Показывается прямая a (слайд 58)).

Проведем через точку O прямую l , параллельную m (слайд 59). (Показывается прямая m (слайд 60)).

Отметим на прямой a точки A и B так, чтобы OA= OB (слайд 61). (Показываются точки A и B (слайд 62)).

Проведем в плоскости a прямую, пересекающую прямые p ,q и l в точках P, Q, L соответственно (слайд 63). (Показывается данная прямая (слайд 64)).

p и q – срединные перпендикуляры к AB . Поэтому AP= BP (слайд 65), (показываются прямые AP и BP (слайд 66)) AQ= BQ (слайд 67), (показываются прямые AQ и BQ (слайд 68))

ΔAPQ = ΔBPQ по трем сторонам (слайд 69). Тогда угол APQ равен углу BPQ (слайд 70).

Проведем отрезки AL и BL (слайд 71). (Показываются отрезки AL и BL (слайд 72)).

ΔAPL = ΔBPL по двум сторонам и углу между ними. Поэтому AL= BL (слайд 73).

Тогда ΔABL равнобедренный (слайд 74). Его медиана LO является его высотой, то есть l ⊥a (слайд 75). Так как l параллельна m и l ⊥ a , то по лемме о перпендикулярности двух параллельных прямых третьей m ⊥ a (слайд 76).

Таким образом, прямая a перпендикулярна к любой прямой m плоскости a , то есть m ⊥ a (слайд 77).

Пусть теперь прямая a не проходит через точку O (слайд 78). (Показывается прямая, не проходящая через точку O (слайд 79)).

Проведем через точку O прямую a 1 параллельную a (слайд 80). (Показывается прямая a 1 (слайд 81)).

По лемме a 1 ⊥ p и a 1 ⊥ q , поэтому по доказанному в первом случае a 1 ⊥ a (слайд 82).

Тогда по теореме о двух параллельных прямых, одна из которых перпендикулярна к плоскости, следует, a ⊥ a (слайд 83).

Пример применения признака перпендикулярности.

Задача 128. Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая OM так, что MA= MC , MB= MD . Докажите, что прямая OM перпендикулярна к плоскости параллелограмма (слайд 84). (Показывается рисунок к задаче (слайд 85)).

Решение (слайд 86)

По условию MA= MC и AO= OC по свойству диагоналей параллелограмма (слайд 87). Поэтому MO – медиана равнобедренного треугольника AMC (слайд 88). Следовательно, MO также высота этого треугольника, то есть MO ⊥ AC (слайд 89).

Аналогично доказывается, что MO ⊥ BD (слайд 90).

Так как MO ⊥ AC и MO ⊥ BD , то MO ⊥ ABCD по признаку перпендикулярности прямой и плоскости (слайд 91).

Литература (слайд 93):

1. Till Tantau User Guide to the Beamer Class, Version 3.07. http://latex-beamer.sourceforge.net, September 29, 2011.
2. Till Tantau The Tikz and PGF Packages, Manual for Version 2.10, http://sourceforge.net/projects/pgf, October, 2010.

Признак перпендикулярности прямой и плоскости. ТЕОРЕМА: Если прямая перпендикулярна к двум пересекающимся прямым,лежащим в плоскости,то она перпендикулярна к этой плоскости. Дано: а ^ р, а ^q,р? a, q ? a, р?q=0. Доказать: а ^ a.

Слайд 13 из презентации «Условие перпендикулярности прямой и плоскости» . Размер архива с презентацией 415 КБ.

Геометрия 10 класс

краткое содержание других презентаций

«Геометрия «Параллельность прямой и плоскости»» - Взаимное расположение прямой и плоскости в пространстве. Свойства. Лемма – вспомогательная теорема. Расположение прямой и плоскости. Параллельность прямых, прямой и плоскости. Определение. Параллельность прямой и плоскости. Признак параллельности прямой и плоскости. Параллельные прямые. Теорема. Прямая и плоскость имеют одну общую точку, то есть пересекаются. Одна из двух параллельных прямых параллельна данной плоскости.

«Декартова система» - Определение декартовой системы. Рене Декарт. Прямоугольная система координат. Введение декартовых координат в пространстве. Понятие системы координат. Координаты точки. Декартова система координат. Координаты любой точки. Вопросы для заполнения. Координаты вектора.

«Равносторонние многоугольники» - Гексаэдр (Куб) Куб составлен из шести квадратов. Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Октаэдр Октаэдр составлен из восьми равносторонних треугольников. Икосаэдр Икосаэдр составлен из двадцати равносторонних треугольников. Додекаэдр имеет 12 граней, 20 вершин и 30 ребер. Октаэдр имеет 8 граней, 6 вершин и 12 ребер. Додекаэдр Додекаэдр составлен из двенадцати равносторонних пятиугольников. Тетраэдр гексаэдр октаэдр икосаэдр додекаэдр.

«Площадь поверхности конуса» - Длина дуги. Радиус основания конуса. Учебник. Как вычислить длину окружности. Тело вращения. Дано. Площадь развёртки. Как выразить величину угла. Измерьте центральный угол развёртки. Вычислите площадь. Конус. Модель конуса. Формула площади полной поверхности конуса. Вычисление площади боковой поверхности модели. Как вычислить длину дуги. Положительные числа. Решение. Задача. Площадь развёртки боковой поверхности конуса.

«Предмет стереометрии» - Сегодня на уроке. Философская школа. Наглядные представления. Планиметрия. Из истории. Евклид. Понятие науки стереометрии. Вселенная. Аксиомы стереометрии. Неопределяемые понятия. Теорема Пифагора. Пифагор. Пентаграмма. Указания. Основные понятия стереометрии. Точки. Египетские пирамиды. Стереометрия. Геометрия. Пространственные представления. Помните ли вы теорему Пифагора. Правильные многогранники.

««Правильные многогранники» 10 класс» - Грани многогранника. Ось симметрии. Цель изучения. Правильные многогранники – самые выгодные фигуры. Фигура может иметь один или несколько центров симметрии. Какое из перечисленных геометрических тел не является правильным многогранником. Правильный додекаэдр состоит из 12 правильных пятиугольников. Элементы симметрии правильных многогранников. Прогнозируемый результат. Центр О, ось а и плоскость.